구조물 기초설계기준 해설
제6장 옹벽
토압은 크게 정지토압, 주동토압 및 수동토압 3가지로 구분되는데 그 구별은 전적으로 옹벽의 변위와 관계된다.
변위가 전혀 없다면 정지토압이 되고
벽체가 뒤채움으로 부터 멀어지는 방향으로 파괴변위를 일으키면 주동토압이 되고
뒤채움쪽으로 파괴변위를 일으키면 수동토압이 된다.
정지상태를 탄성평형상태라고 하며, 주동 및 수동상태를 소성한계상태라고 한다.
토압계수는 수평유효응력에 대한 연직유효응력의 비(sigma_h / sigma_v)로 정의된다.
변위를 전혀 허용하지 않는 옹벽이 경우는 정지토압으로 설계되어야 한다.
옹벽과 뒤채움 흙과의 마찰각(벽면마찰각)과 옹벽연직변위도 주동토압에 영향을 끼친다.
벽면마찰각에 따른 주동토압크기의 영향은 옹벽이 연직으로 많은 침하를 일으키지 않는다면 크지 않으나 수동토압에 미치는 영향은 매우 크다.
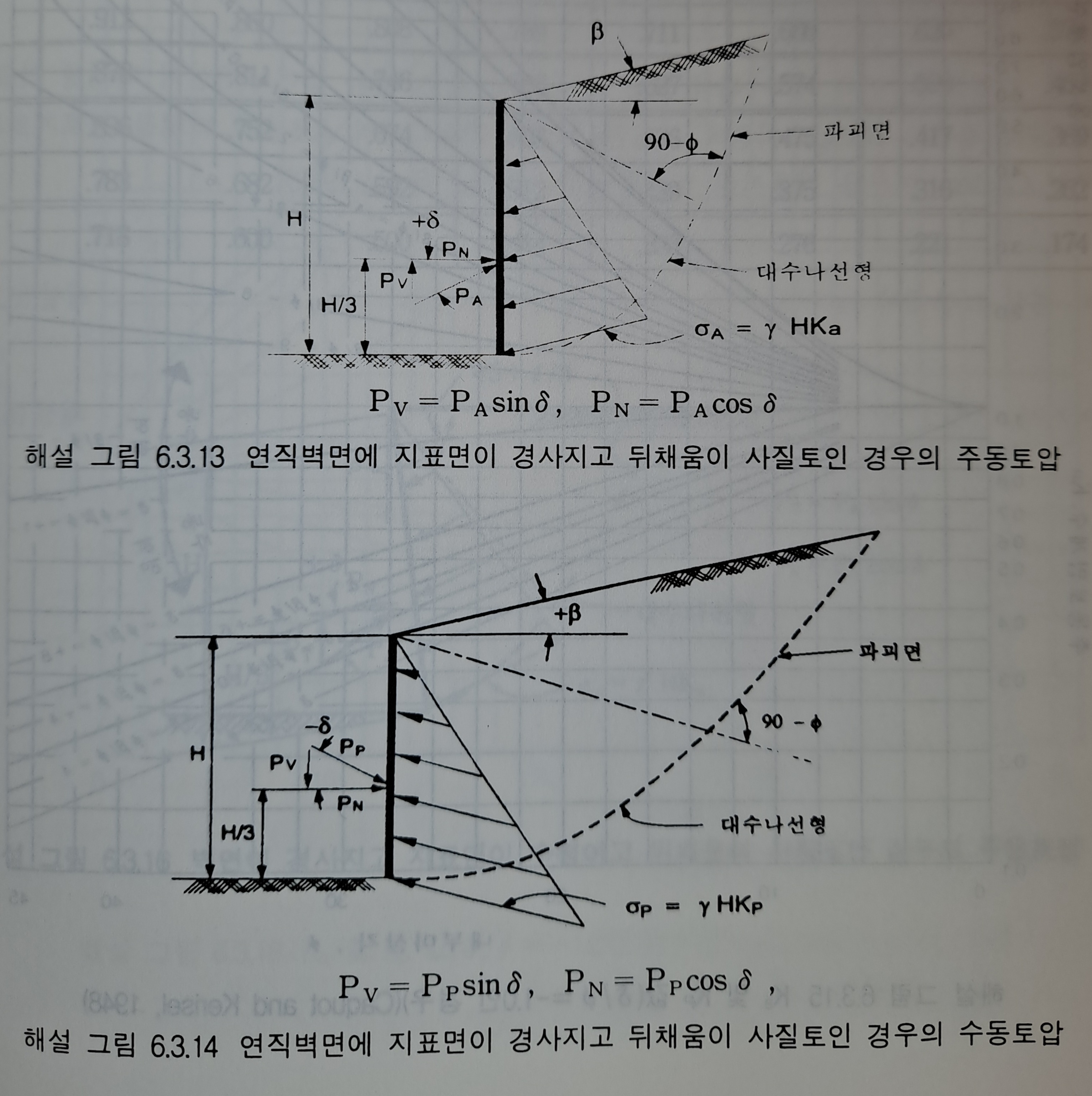
옹벽이 침하하지 않으면 해설 그림 6.3.13에서 보는 바와 같이 주동토압은 벽면마찰각이 (+)로 작용하여 감소하고 수동토압은 해설 그림 6.3.14에서와 같이 아래(-)로 작용하여 증가한다.
토압공식에는 Coulomb, Rankine, Terzaghi의 공식 등 여러 식이 있지만 실내외 실험 결과 Coulomb의 토압공식이 비교적 측정치에 가까운 값을 보이기 때문에 Coulomb의 토압공식을 사용하기로 한다.
그러나 강널말뚝 등 변형하기 쉬운 구조물에 작용하는 토압은 복잡한 곡선분포를 보이므로 이 경우에는 coulomb의 토압을 사용해서는 안된다. 그리고 역 T형 옹벽 또는 부벽식 옹벽과 같이 토압이 뒷굽에서부터 위로 연직하게 세운 가상면에 작용할 때에는 Rankine 토압을 사용한다. 그 이유는 옹벽구조물이 회전하거나 밀려나는 경우에도 이 가상면을 따라서 전단이 일어나지 않기 때문이다.
벽면 마찰각의 부호는 주동토압의 경우에는 정(正), 수동토압의 경우에는 부(負)를 취하기로 한다. Coulomb의 수동토압은 (-theta), (-delta)의 값이 크면 과대하게 되므로 수동토압 계산의 제공식의 적용에는 다음과 같은 제한을 둔다. 즉, (-delta)의 값은 배면토의 전단저항각의 1/3이하로 하고 (-theta)의 값은 최대 20degree로 한다.
점성토의 경우에는 주동토압과 수동토압 계산에 점착력을 영향을 고려한다.
일반적으로 점성토는 함수비에 이해 현저하게 그 성질이 변화한다. 따라서 구조물이 설치된 후 배면인 점성토의 성질을 정확히 추정하기는 어렵다. 즉, 설계시에 현위치시험 혹은 채취시료에 의한 실내시험의 결과에서 점착력을 구해도 그 당시의 값을 아는 것에 불과하므로 이러한 이유들 때문에 흙의 점착력을 정확히 추정할 수 없는 경우에는 점착력의 영향을 무시하고 전단저항각을 작게 잡아 토압계수를 작게 잡아 토압계수를 구하는 것이 좋다.
[2] 뒤채움 공간이 제한되어 있는 경우
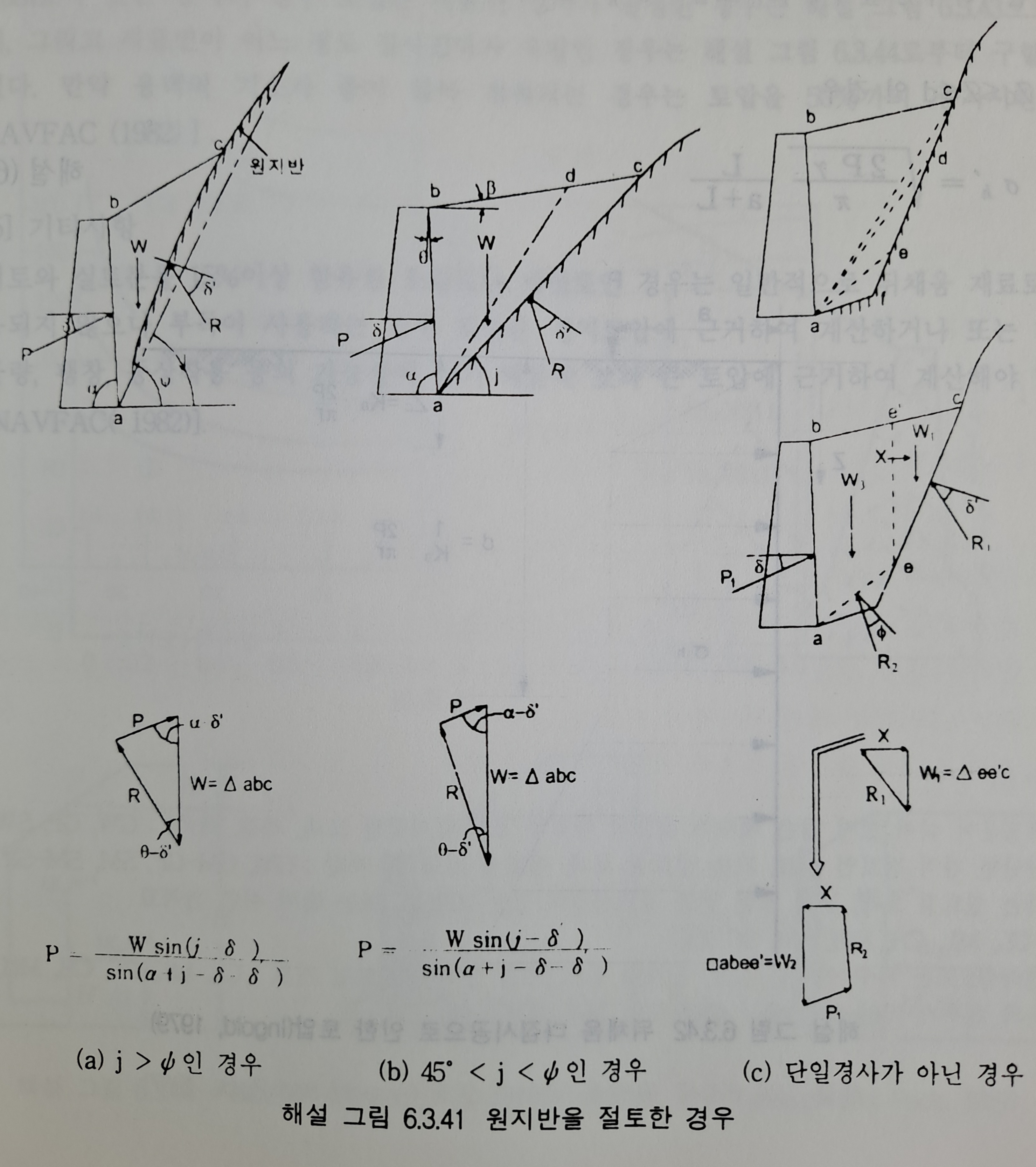
옹벽 배면의 원지반을 절토한 경우, 즉 원지반의 경사가 45degree이상이고, 옹벽 뒷굽과 해설 그림 6.3.42와 원지반하단의 수평거리가 1.0m 이하인 경우 옹벽에 작용하는 토압은 그 경계면의 영향을 받기 때문에 일반적인 성토부 옹벽에 작용하는 토압과는 다르게 취급해야 할 경우가 있다. 이 경우 원지반은 안정되어 있는 것으로 간주하여 옹벽과 그 경계면의 위치, 원지반의 경사, 그 표면의 거친정도 등에 따라 토압이 달라지는데 보통의 성토부 옹벽에 작용하는 토압과 비교하여 크게 되는 경우가 있으므로 주의해야 한다. 이 경우 토압크기는 해설 그림 6.3.41에 나타난 것과 같은 도해법이나 계산식으로 구할 수 있으며 토압의 작용위치는 옹벽저면에서 H/3(H:옹벽높이) 되는 곳이다.
활동파괴면과 뒤채움 흙과의 마찰각(delta')의 크기는 원지반의 지질이나 표면상태에 따라 다르지만 통상 (2/3~1.0)phi로 볼 수 있으며 원지반이 연암보다 좋고 비교적 균일한 평면인 경우는 delta'=2/3phi, 원지반이 층이 있고 거친면인 경우 delta'=phi로 간주할 수 있다. 이 delta'의 크기에 따라 토압크기에 영향이 크므로 delta'의 결정에는 신중하여야 한다. 원지반의 경사가 해설 그림 6.3.41(a)(b)와 같이 단일 경사인 경우 원지반의 경사각 j가 가상활동파괴면의 경사각에 비해서 큰가 작은가에 따라서 토압을 달리 구한다. 이 때 는 Coulomb의 평면활동 파괴면의 가정에 의해 해설(6.3.32)식으로 나타낸다.
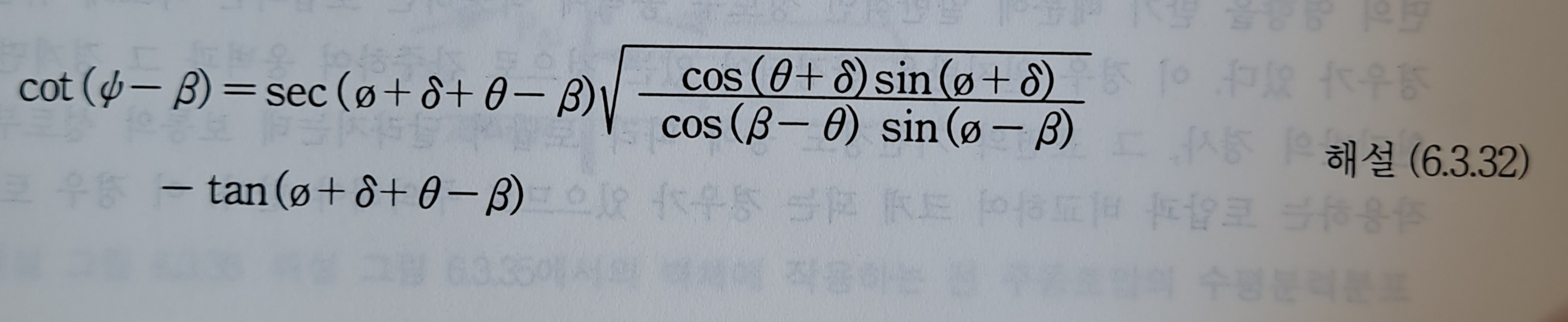
여기서
beta : 뒤채움 흙의 지표면 경사각
theta : 옹벽 배면의 경사가 연직면과 이루는 각
delta : 벽면 마찰각
phi : 뒤채움 흙의 내부마찰각











최근댓글